第一章
1. Sigmoid neurons
该激活函数的特点是变化平缓,输入的微小改变不至于导致输出结果的巨大变化,这样才能让神经网络更好的学习,也能更好的适应于新的数据输入(从已有的外推新的时不会造成造成认知的巨大变化,已有的经验才能适用,有点像 A 学会一题解法,但是条件变一下就不会了,而 B 却能举一反三,这里就是希望算法具备 B 的特质),使算法具备更高的鲁棒性。
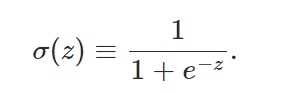
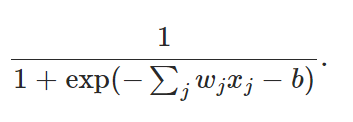
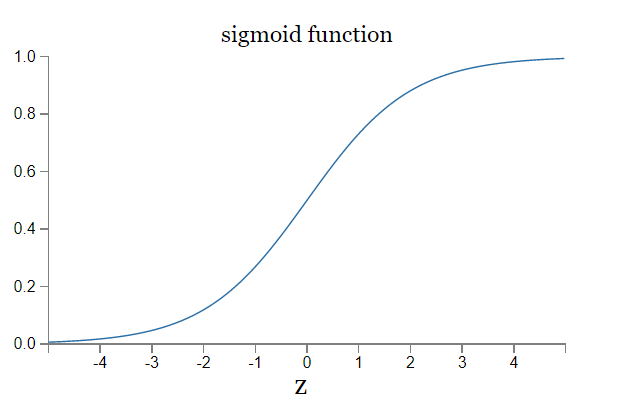
2. cost function
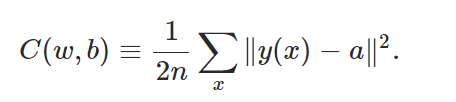
上式中 x 是输入向量,y 是对应于该输入的准确解向量,a 是对应于 x 的神经网络计算值;本质上 C 是关于 w, b 的一个函数,我们需要找到一组 w,b 值,是的对于任意输入的 x 向量,C 的值会很小,也就是预测值与真实值接近。而这是通过找到对于训练集(一个 x 的集合)所有 x 都能达到较好的估计效果的一组 w,x 来实现的。通过训练,让程序针对这一类问题掌握某种规律,从何应对从未接触过的新的同类问题。
解决上述问题的关键归结到找 C 函数的最小值,此处用到了梯度下降法
3. gradient descent
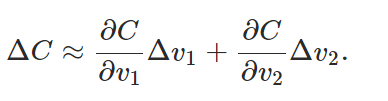
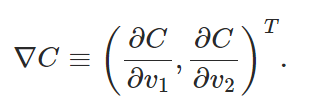
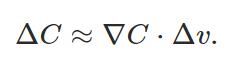
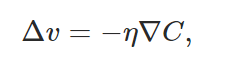
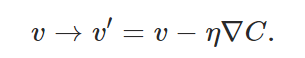
大致总结为:
计算 C 关于各个自变量的偏导;
取各变量的增量为一个系数(eta)乘上前面求得的偏导再去相反数,如此 C 的变化肯定是负数了,也就是下降了;这里 η 的选取是很重要的,因为这关系到第一个式子是否成了,也就是 C 能不能真的减小;
由此可以计算出一个新的 V 向量,也就朝“山坡”向下迈了一步,然后在这一个新的位置,继续上述过程,直到找到一个最低点。
4. stochastic gradient descent
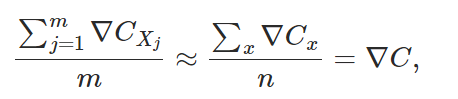
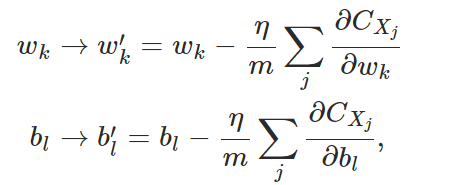
由于需要找到的时一组对于所有 x 输入都比较适用的 w,b 值,因此需要考虑对于每个 x 输入求得一个梯度下降系数之后取个均值,但是这样未免太慢了点,不如把输入集分成很多同样大小的小集合,对一个小集合算出一个上述的均值梯度系数,算完后可以得到一组新的 w,b 值,也就是新起点;再在此基础上对下一个小集合继续算均值梯度系数,这样迭代下去,慢慢更新 w,b 值,直至算完所有小集合。