学习笔记 | LEO | 2022-01-15 |

傅里叶变换

傅里叶变换及其MATLAB实现的详细资料

https://www.utdallas.edu/~dlm/3350%20comm%20sys/FFTandMatLab-wanjun%20huang.pdf

https://zhuanlan.zhihu.com/p/19763358

以下内容根据UP主DR_CAN相关系列视频总结

https://space.bilibili.com/230105574/channel/seriesdetail?sid=1569597

正交三角函数系

$$
sinx,sin2x,sin3x…\\
1,cosx,cos2x,cos3x…
$$

上面的公式中任意两个相乘，在$-\pi$到$\pi$（或其他长度为$2\pi$的区间）上的积分为0。具体证明参考https://zhuanlan.zhihu.com/p/341796771

周期函数傅里叶展开

对于周期为$2\pi$的函数可以通过上面的正交三角函数系进行表示，如后面的式子所示，系数可以通过左右两边同乘$cosnt$或$sinnt$再对两边积分求得；

而对于周期不是$2\pi$的函数，可以通过变量代换进行转化，最终可得一般情况的傅里叶展开式如下

一个周期为T$(\omega_0 = \frac{2\pi}{T})$的函数表示为无数个正交三角函数求和：

$$
f(t) = \frac{a_{0}}{2} + \sum_{1}^{\infty }(a_{n}cosn\omega_0 t + b_{n}sinn\omega_0 t )
$$

其中系数的表达式为：

$$
a_{0} =\frac{2}{T}\int_{0}^{T}f(t)dt \\
a_{n} = \frac{2}{T}\int_{0}^{T}f(t)cosn\omega_0 tdt \\
b_{n} = \frac{2}{T}\int_{0}^{T}f(t)sinn\omega_0 tdt
$$

复数表达形式

欧拉公式：$ e^{i\theta} = cos\theta + isin\theta$

通过欧拉公式改写：

$$
cos\theta = \frac{e^{i\theta} + e^{-i\theta }}{2} \\
sin\theta = \frac{e^{i\theta} - e^{-i\theta }}{2}
$$

将上式代入到前面的傅里叶展开式中得到复数表达形式：

$$
f(t)=\sum_{n=-\infty}^{\infty } C_ne^{in\omega_0 t}\\
C_n = \frac{1}{T}\int_{0}^{T} f(t)e^{-in\omega_0 t}dt
$$

傅里叶变换（FT）

对于非周期函数，可以认为周期无穷大，即T→∞，

将$C_n$表达式代入，得：

$$
f(t)=\sum_{n=-\infty}^{\infty } \frac{1}{T}\int_{0}^{T} f(t)e^{-in\omega_0 t}dte^{in\omega_0 t}\\
\Delta \omega = (n+1)\omega_0 - n\omega_0 = \omega_0 = \frac{2\pi }{T}\\
\frac{1}{T} = \frac{\Delta \omega}{2\pi} \\
$$

$$
f(t) =\int_{-\infty}^{\infty }\frac{d\omega }{2\pi }\int_{-\infty }^{\infty } f(t)e^{-i\omega t}dte^{i\omega t}
=\frac{1 }{2\pi }\int_{-\infty}^{\infty }\int_{-\infty }^{\infty } f(t)e^{-i\omega t}dte^{i\omega t} d\omega
$$

这里注意当T区域无穷大时，是要对整个区间进行积分的，因为整个区间构成一个周期。

$$
F(\omega) = \int_{-\infty }^{\infty } f(t)e^{-i\omega t}dt\\
$$

$$
f(t) = \frac{1}{2 \pi}\int_{-\infty }^{\infty } F(\omega)e^{i\omega t}d\omega
$$

上面第一式即为f(t)的傅里叶变换，下式为傅里叶逆变换。

离散傅里叶变换（DFT）(参考）

当函数不是连续的，而是由许多离散点构成的时候，有以下公式

$$
X(k)=\sum_{k=0}^{N-1 } x(n)W_N^{nk}\\
x(k)=\frac{1}{N} \sum_{n=0}^{N-1 } X(k)W_N^{-nk}\\
其中：W_N = e^{-i\frac{2\pi}{N} }
$$

快速傅里叶变换（FFT）

利用$W_N^{nk}$的性质对离散傅里叶变换的计算进行简化，使运算效率得到极大地改进

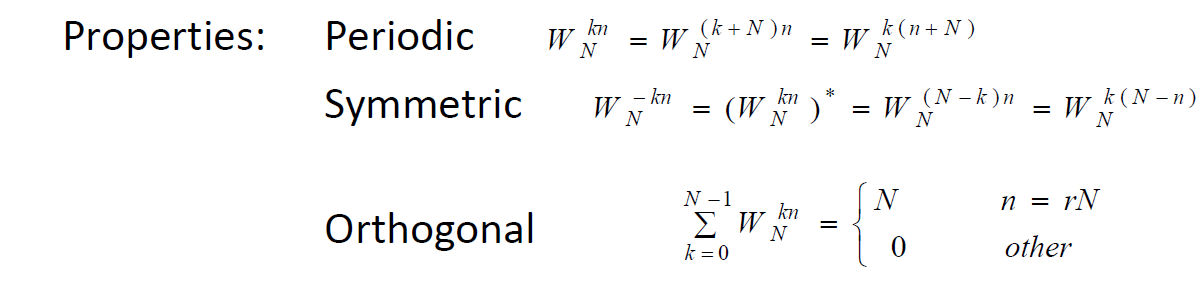
将前述离散傅里叶变换公式分成奇数项和偶数项两部分求和，从而将数据点减少一半，如此递归进行，直到只剩一个数据点

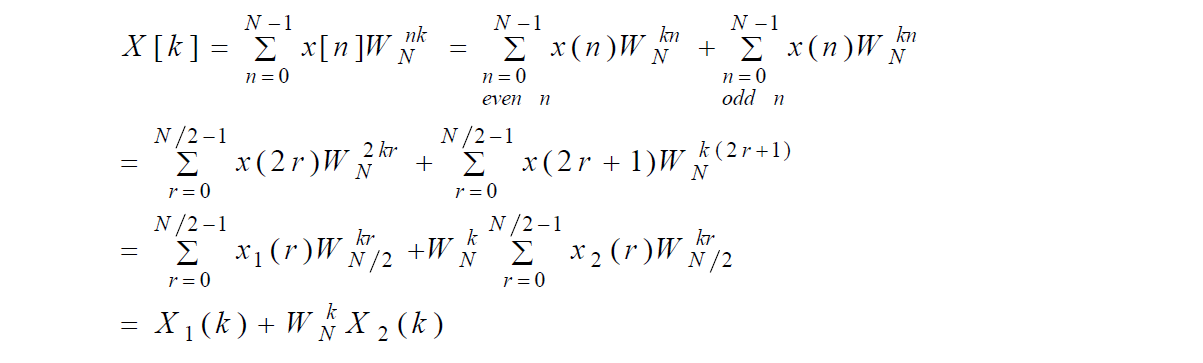
为什么FFT后幅值要除以N/2

https://zhuanlan.zhihu.com/p/137433994

深入理解DFT的原理

https://www.bilibili.com/video/BV1Tb41187i1?from=search&seid=7850258132860582140&spm_id_from=333.337.0.0

如何得到一个余弦信号的频率
给定一个离散余弦函数如下，称样本函数：
$$
x[n] = cos(2\pi \frac{2n}{40}) \quad n = 0,1,2…,39
$$ 它的图像为：
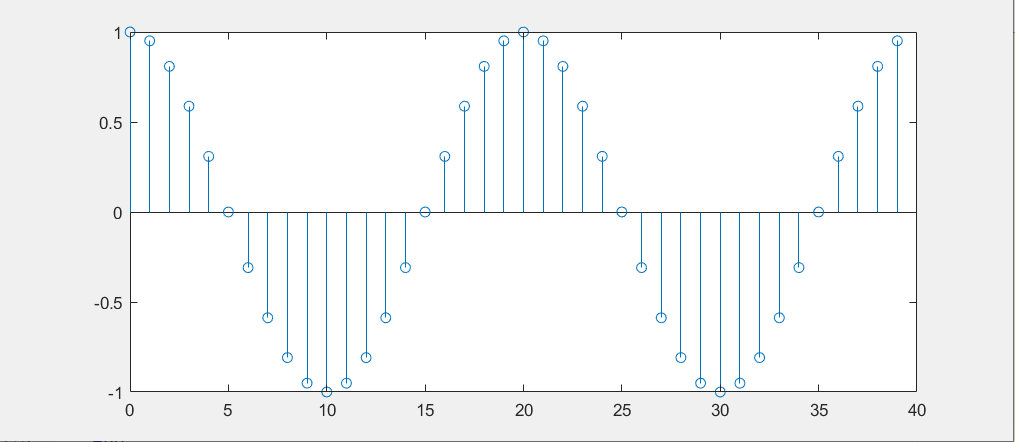注意：此处不涉及时间，横坐标只是点的计数，图中并不能反映这个余弦波持续的时间，需要后面加上采样频率的限定才能确定时间的长度。
我们人眼可以从上图看出这个波在40个采样点内振荡了两个周期，但是计算机必须采用别的方式来“看”。
利用三角函数系的正交性做相关性比较
给定一系列振荡频率依次增加的基函数：
$$
x[0] = cos(2\pi \frac{0}{40}) \\
x[1] = cos(2\pi \frac{1}{40}) \\
x[2] = cos(2\pi \frac{2}{40}) \\
…\\
x[39] = cos(2\pi \frac{39}{40})
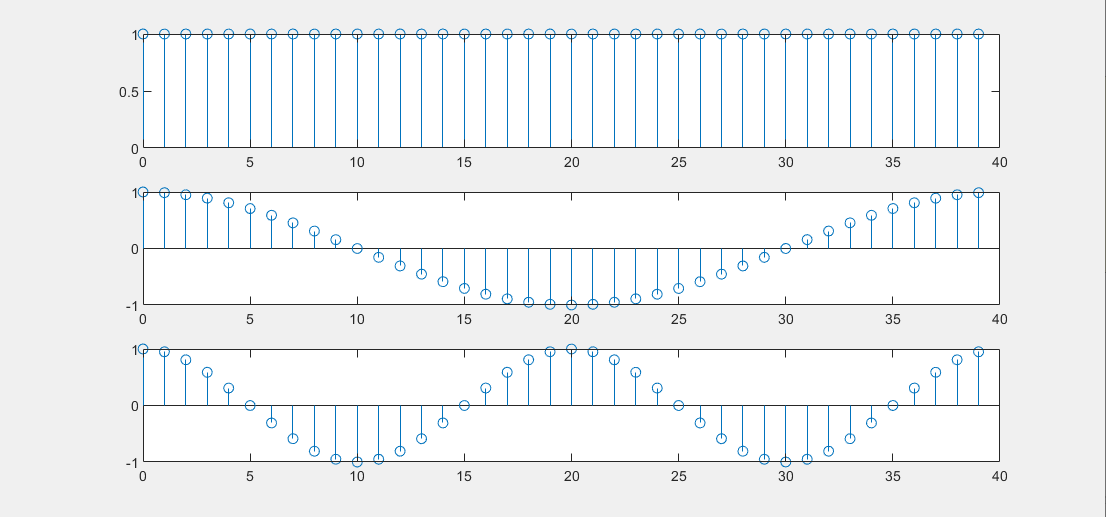
$$
用这些基函数与样本函数在采样点出做内积，记为：
$$
X[k] = \sum_{n=0}^{39}cos(2\pi\frac{2n}{40})cos(2\pi\frac{kn}{40})
$$ 由于正交性，只有X[2]和X[38]（两者相加和为$2n\pi$)不为0，其他结果都为0；
$$
X[2] = X[38] = 20;
$$ 画出X[k]的图像如下：

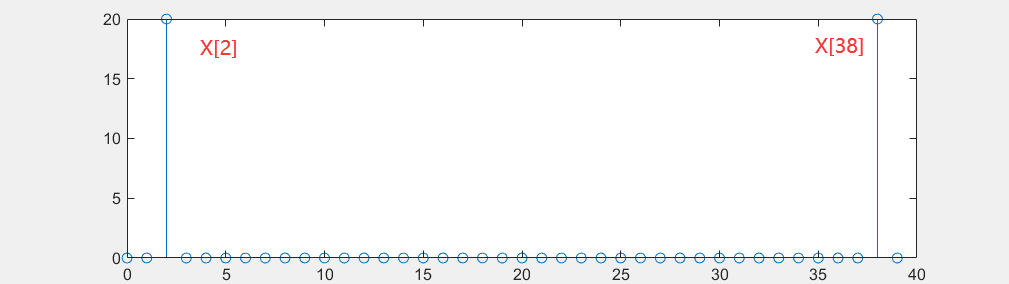
如此，我们就可以根据基函数来确定样本函数中的k值，即给定的采样点内振荡的周期数。
对上面的内积公式一般化，即对于一般的采样点数N，以及一个样本函数x[n]，有：
$$
X[k] = \sum_{n=0}^{N-1}x[n]cos(2\pi\frac{kn}{N})
$$ 观察发现，这个离散傅里叶变换的公式是很相似的：
$$
X[k] = \sum_{n=0}^{N-1}x[n]e^{-2\pi j \frac{kn}{N}}
$$ 用欧拉公式对上式进行展开可得：
$$
X[k]=\sum_{n=0}^{N-1} x[n] \cos \left(2 \pi \frac{k n}{N}\right)-j \sum_{n=0}^{N-1} x[n] \sin \left(2 \pi \frac{k n}{N}\right)
$$ 多出的右边一项是用正弦函数sin做内积得到的，它可以与cos内积结果结合起来得到原函数的相位信息
结合正弦函数做内积获取相位信息
单纯使用cos是丢失了信息的，比如原先的函数有一个初始相位$\pi/3$,和原来的函数幅值减半两者得到的X[k]图像是一样的，
$$
x_1 = cos(2\pi \frac{2n}{40} + \pi/3) \\
x_2 = \frac{1}{2}cos(2\pi \frac{2n}{40})
$$
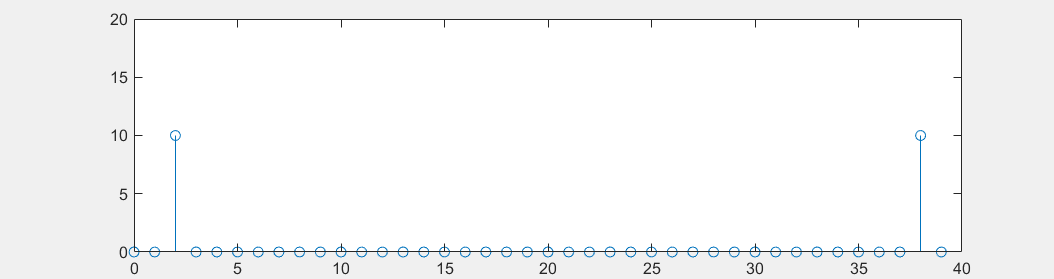
如果用sin函数去做内积得：
$$
X_{sin}[2] = \sum_{n=0}^{39}sin(2\pi\frac{2n}{40})cos(2\pi\frac{2n}{40} + \pi/3) = 10\sqrt{3} \\
X_{sin}[38] = \sum_{n=0}^{39}sin(2\pi\frac{38n}{40})cos(2\pi\frac{2n}{40} + \pi/3) =-10 \sqrt{3} \\
$$ 结合前面的cos结果：
$$
X_{cos}[2] = \sum_{n=0}^{39}cos(2\pi\frac{2n}{40})cos(2\pi\frac{2n}{40} + \pi/3) =10 \\
X_{cos}[38] = \sum_{n=0}^{39}cos(2\pi\frac{38n}{40})cos(2\pi\frac{2n}{40} + \pi/3) =10
$$ 可以得到幅值和相位信息：
$$
mag = \sqrt{10^2 + (10\sqrt{3})^2} = 20 \\
acrtan\psi = \sqrt{3} \quad => \psi = \pi/3
$$

背后的原理

为此可以将两个内积结果通过复数来组合（实质为将两组信息存储在一个数中)
因此定义新的X[k]为：
$$
X[k]=X_{cos}[k] - jX_{sin}[k] \\ = \sum_{n=0}^{N-1} x[n] \cos \left(2 \pi \frac{k n}{N}\right)-j \sum_{n=0}^{N-1} x[n] \sin \left(2 \pi \frac{k n}{N}\right)
$$ 此即为离散傅里叶变换公式的内涵。
给定采样频率
前面给出的样本函数只是一些离散的点，只知道它跨越了几个周期，但是不知道周期是多少，所以在实际问题中，还需要确定采样频率$f_s$

采样频率：1s内采样点的个数

如前面采样点为40，如果采样频率为100，即1s采样100个点，那么40个点对应的时间长度为0.4s，它跨越了两个周期，因此样本函数的周期T为0.2s，频率为5Hz。
一般地，设采样点数为N，采样频率为$f_s$，周期数为k，则可以计算出样本函数的频率为：
$$
T = \frac{N}{f_s k} \quad f = \frac{f_sk}{N}
$$ 根据前面那个例子，设采样频率为4000，则有k=2和k=38两处的频率值分别为200和3800Hz，但是3800这个频率是不对的，因为40个采样点振荡38个周期，那获取的信息是不足的，要获取一个信号的全部信息，必须在一个周期内至少采样2次。对于实数信号，我们只需关心前一半的频率范围。
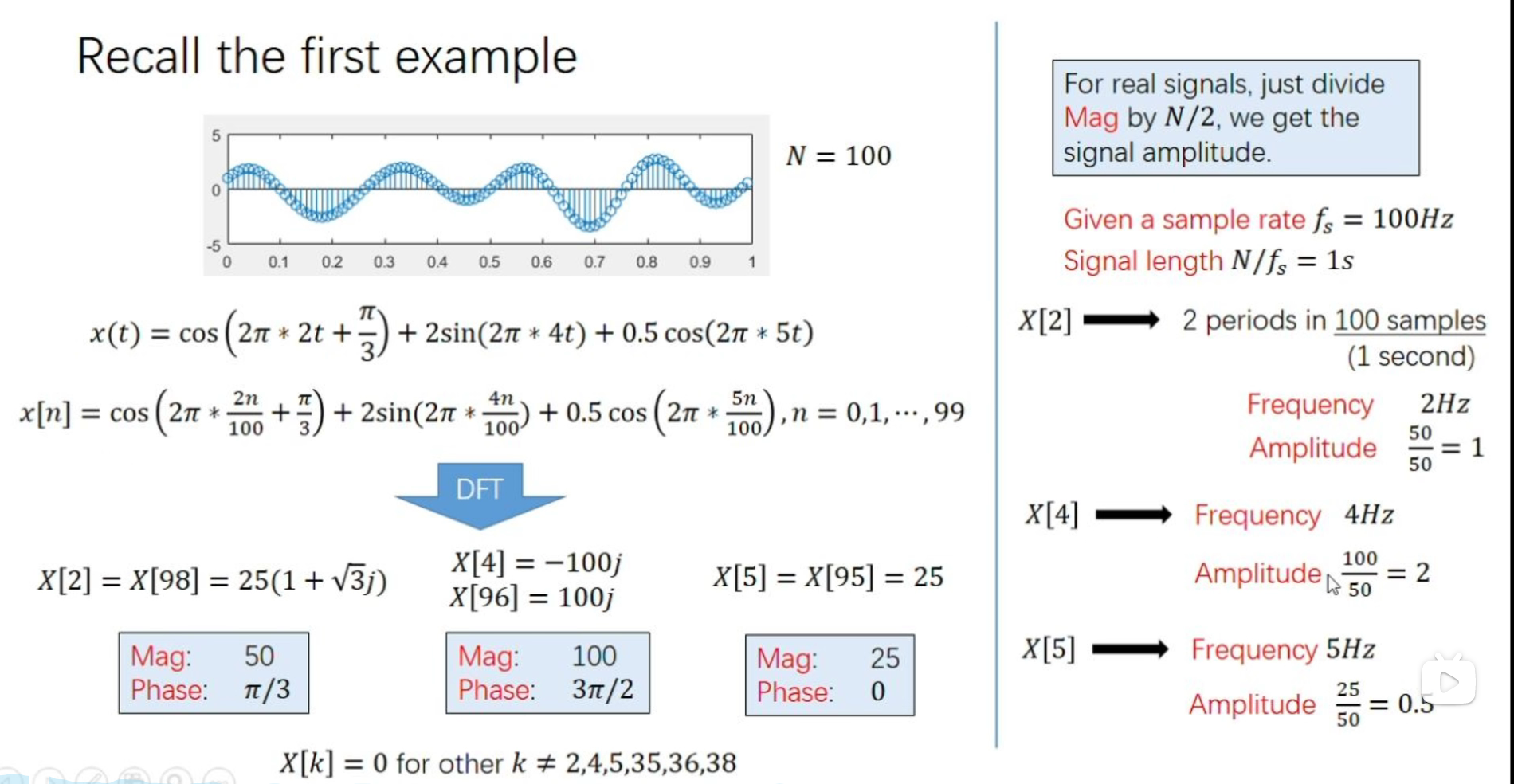
FFT之后得到的一系列复数，是波形对应频率下的幅度特征，注意这个是幅度特征（特征值）不是幅值。
对于实信号，要得到原样本函数的幅值，只需将各频率处的幅值除以N/2即可，具体原因如下：

幅值除以N/2简单证明
以cos基函数为例（sin同理），设样本函数幅值为A，与和它同频的基函数相乘求和得
$$
\sum_{n=0}^{N-1}Acos(2\pi\frac{kn}{N})cos(2\pi\frac{kn}{N}) = A\sum_{n=0}^{N-1}\frac{cos(4\pi\frac{kn}{N}) + 1}{2} = A\frac{N}{2}
$$

上式中 $k\ne$0和$\frac{N}{2}$,事实上，等于这两个值的时候结果为AN，因此截取一半频率范围后，首尾两个频率处应该除以N。

实例：

Matlab函数fft简单示例代码

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
Y = fft(S);
f = Fs*(0:(L/2))/L;
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

plot(f,P1) 
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

tags: #傅里叶变换 #数学 #MATLAB

傅里叶变换学习笔记